Fibonacci and Lucas Numbers1
“The numbers are by him [Plato] expressly identified with the Forms themselves or principles, and are formed out of the Elements (i.e., Principles of the One and Indefinite Dyad).”
-Aristotle, De Anima 404b24.
Nature widely expresses the golden ratio through two very simple series of whole numbers. The numbers in both the Fibonacci number series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377... [177] and the Lucas number series: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199… [178] are additive, as each number is the sum of the previous two, and multiplicative, as each number approximates the previous number multiplied by the golden ratio. The ratio between any two adjacent numbers approximates the Greater golden ratio, Φ, when dividing the larger number by the smaller, asymptotically becoming more accurate as the numbers increase. Inversely, any number divided by its larger neighbor approximates the Lesser golden ratio, ϕ, alternating as more or less than ϕ, asymptotically becoming more accurate as the numbers increase. Each Fibonacci or Lucas number is the approximate geometric mean of its two adjacent numbers.
For Fibonacci numbers one has to alternately add or subtract 1. For example, 3, 5, 8: 5 =  ; 5, 8, 13: 8 =
; 5, 8, 13: 8 = 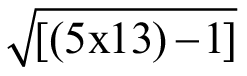 .
.
For Lucas numbers one has to alternately add or subtract 5. For example, 3, 4, 7:
4 = 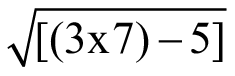 ; 4, 7, 11: 7 =
; 4, 7, 11: 7 = 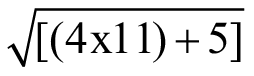 .
.
From an ontological (top down) perspective, the Greater and Lesser are ontological prenumber principles that give rise to all integers, through addition, subtraction, multiplication or division. Fibonacci and Lucas numbers have special relations to the Greater and Lesser as shown in tables 1 and 2 below. Lucas numbers have an extremely interesting formula: they alternate between adding and subtracting the successive exponential golden powers of the Greater and Lesser. All non-Lucas and non-Fibonacci integers are easily seen to be composed of the powers of the Greater and Lesser. For example, one can easily see several ways in which the powers could be combined to give rise to numeral 6 [e.g. (G2 + L2) + (G2 + L2) = 3 + 3 = 6]. Likewise, the number 12 could arise through several combinations of the powers [e.g. (G5 – L5) + (G1 – L1) = 11 + 1 = 12], etc.
To the objection that an exponent, say 5 in a formula that includes Lesser5 (i.e. L5 in a formula like G5 – L5 = 11) already requires the integer 5, we reply that it is simply the fivefold iteration of the Lesser, i.e. L x L x L x L x L. It is equally legitimate to point out that the exponent 5 is simply the sum of two Lucas formulas of (G3 – L3) + (G1 – L1) = 4 + 1 = 5. Or we could use the Fibonacci formula for 5, G3 + 2L2 = 5. Here again one might object that the coefficient 2 is involved in the formula. But again, 2L2 is simply L2 + L2, or we can use the Lucas formula for 2, G0 + L0 = 2, or the Fibonacci formula for 2, G1 + L2 = 2. In the end, all integers are reducible to sums, differences, multiples and divisions of the Greater and Lesser in their capacity as prenumber principles. It is of course true that from an epistemological (bottom up) perspective we can calculate the numerical value of the Greater and Lesser with the formulas
Φ = 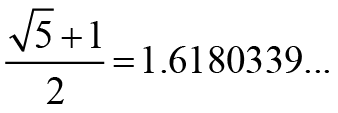 and ϕ =
and ϕ =  .
.
So, it is very important that we clarify this distinction between perceiving the Indefinite Dyad on the one hand as inherent pre-numerical powers of construction resulting from the initial ontological asymmetric golden cut in the beginning as seen from a macroscopic, holistic (top down) view, and on the other hand as the relative numerical values of these powers looked at and calculated epistemologically from a more piecemeal, fragmented (bottom up) view.

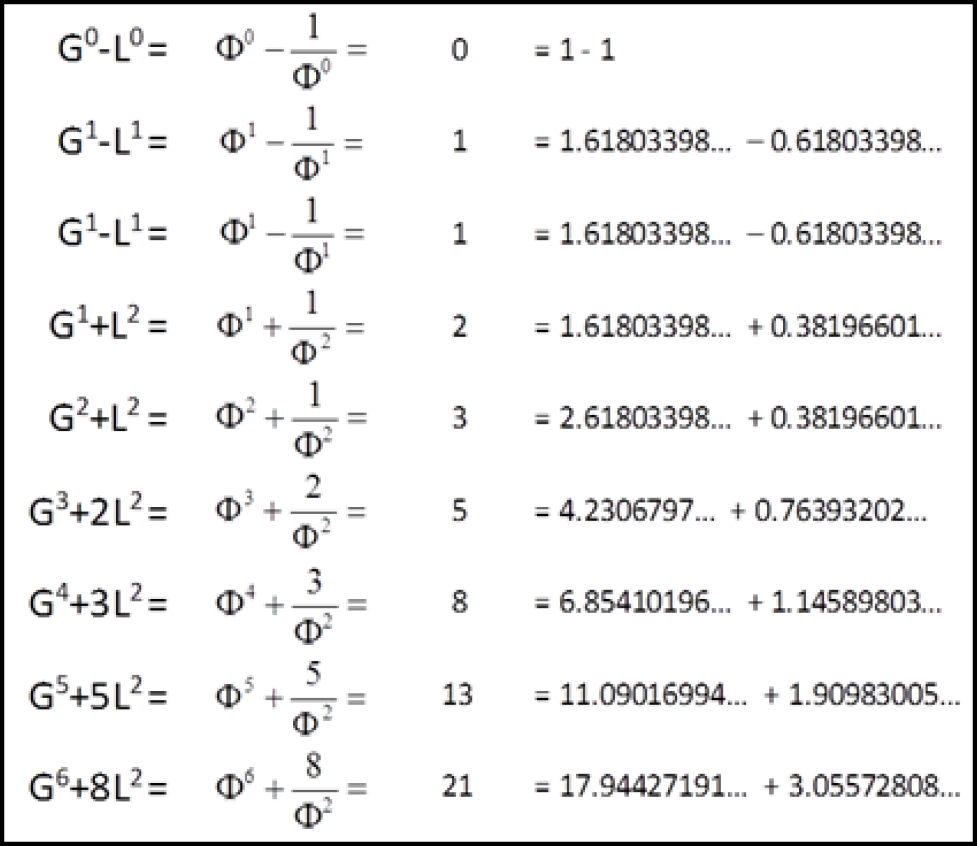


1 For a further explanation of the history, nature and application of Fibonacci and Lucas numbers, see Olsen, 2006, The Golden Section [72].